Ein Großteil der digitalen Display-Werbung beinhaltet heutzutage die Vorhersage der Wahrscheinlichkeit eines Klicks oder einer anderen Benutzeraktion, wie z. B. eines Kaufs. Der gängigste Algorithmus für maschinelles Lernen zur Vorhersage der Click-Through-Rate (CTR) ist die logistische Regression (LR).
Beim Real Time Bidding (RTB) für einen bestimmten Anzeigenplatz auf einer Webseite werden die Merkmale, wie Browser, Region, Gerätetyp usw., von einem LR-Modell zur Berechnung der Klickwahrscheinlichkeit verwendet. Diese Wahrscheinlichkeit beeinflusst, ob ein Gebot abgegeben wird und wie hoch dieses Gebot sein wird. Falsche Vorhersagen können zu hohen Kosten pro Klick führen, was sich in niedrigen Margen und unzufriedenen Kunden niederschlägt.
Die logistische Regression ist schnell, was bei RTB wichtig ist, und die Ergebnisse sind leicht zu interpretieren. Ein Nachteil von LR ist, dass es sich um ein lineares Modell handelt, sodass es bei mehreren oder nicht linearen Entscheidungsgrenzen unterdurchschnittliche Leistungen erbringt. Betrachten Sie z. B. einen Fall, in dem die Daten nur aus zwei Features mit jeweils zwei Werten bestehen, wie in Abbildung 1 dargestellt. In diesem Szenario ist es unmöglich, eine gerade Linie so zu zeichnen, dass sich die Positiven auf der einen Seite und die Negativen auf der anderen Seite befinden. Eine Möglichkeit, diese Linearitätsbeschränkung zu umgehen, besteht darin, die Merkmalsvektoren in einen höherdimensionalen Raum zu konvertieren, indem Merkmalsinteraktionen eingeführt werden. Es könnte ein drittes Feature namens "Hour-Domain" hinzugefügt werden. Dadurch wird der Merkmalsvektorraum dreidimensional, wie in Abbildung 2 dargestellt.
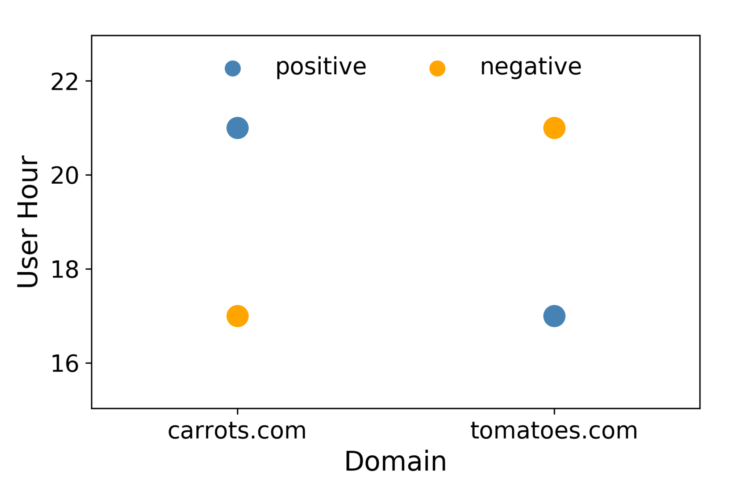
Abbildung 1: Für dieses Szenario gibt es keine gute lineare Entscheidungsgrenze.
Jetzt kann eine Ebene gezeichnet werden, um die Positiven von den Negativen zu trennen. Mit ein bisschen Feature-Engineering können wir LR also dazu bringen, Beziehungen zwischen Merkmalspaaren zu lernen. Das hat allerdings seinen Preis. Das Hinzufügen von Merkmalsinteraktionen erhöht die Komplexität eines Modells auf O(n2), wobei n die Gesamtzahl der Werte in einem Datensatz ist.
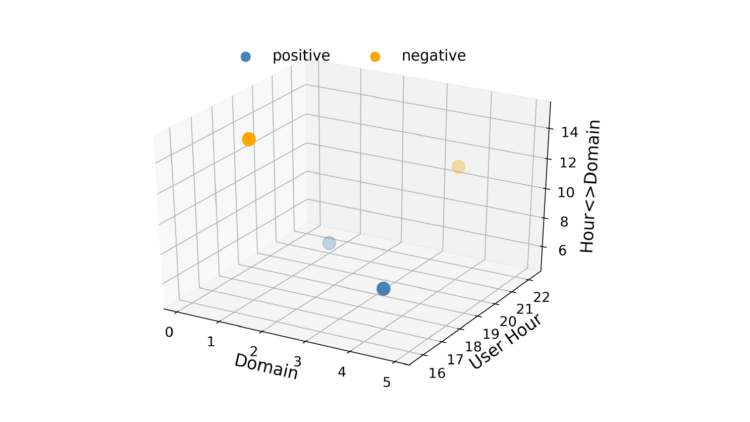
Dies ist unpraktisch für CTR-Vorhersagen, wo ein Modell Tausende von Werten haben könnte. Wenn ein Wertepaar in einem Datensatz nicht vorhanden ist, kann die logistische Regression auch nicht die Stärke der Interaktion lernen. Factorization Machines (FM) [1, 2] lösen diese beiden Probleme.
Was sind Faktorisierungsmaschinen?
Um diese Frage zu beantworten, ist es hilfreich, die Matrixfaktorisierung, auch Matrixzerlegung genannt, zu kennen. Es ist einfach die Zerlegung einer Matrix in ein Produkt aus mehreren anderen Matrizen. Mit anderen Worten, die Matrixfaktorisierung ist einfach ein mathematisches Werkzeug, um mit Matrizen herumzuspielen, um etwas herauszufinden, das unter den Daten verborgen ist. Die Hauptkomponentenanalyse (PCA) ist ein Beispiel für ein Matrixfaktorisierungsmodell.
Normalerweise ist es nicht trivial, einen Faktorisierungsansatz auf ein neues Problem anzuwenden. Faktorisierungsmaschinen machen es viel einfacher, weil sie ähnliche Ergebnisse wie andere Faktorisierungsmodelle erzielen können, indem sie einfach Feature-Engineering verwenden [3]. Werfen wir einen Blick auf die Kostenfunktion, die bei der linearen CTR-Vorhersagemodellierung verwendet wird.
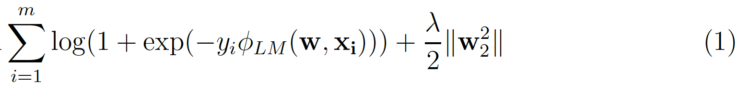
m ist die Anzahl der (xᵢ, yᵢ) Instanzen in einem Datensatz, wobei yᵢ das Klick/Nicht-Klick-Label ist und xᵢ ist die n-dimensionalen Merkmalsvektor. Der zweite Term ist der L₂-Regularisierungsterm, wobei ƛ ist die Stärke der Regularisierung. Für logistische Regression
Das Hinzufügen von Wechselwirkungen führt einen weiteren Begriff ein.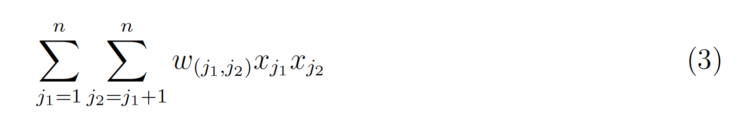
w(j₁ ;j₂) ist das LR-Gewicht für die Interaktion, es wird also für jedes einzelne Interaktionspaar ein Gewicht gelernt. Der Trick der Factorization Machines besteht darin, ein k-dimensionalen latenten Vektor für jedes Merkmal zu lernen, wobei k ein benutzerdefinierter Parameter ist. Der Interaktionseffekt kann dann einfach berechnet werden, indem das innere Produkt der beiden Vektoren genommen wird.
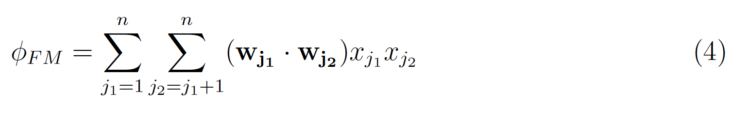
die umgeschrieben werden kann als
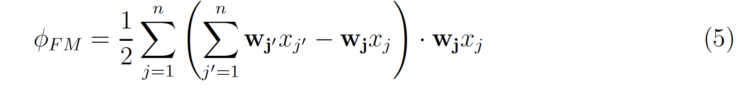
Die Komplexität der obigen Gleichung ist nur O(nk), wobei n die durchschnittliche Anzahl von Nicht-Null-Werten pro Instanz ist.
Logistische Regression vs. Faktorisierungsmaschinen
Wir haben die Implementierung von Factorization Machines von AWS Sagemaker verwendet, um FM an unseren Daten zu testen. Informationen zu den Daten für die fünf verschiedenen analysierten Werbetreibenden sind in Tabelle 1 aufgeführt.
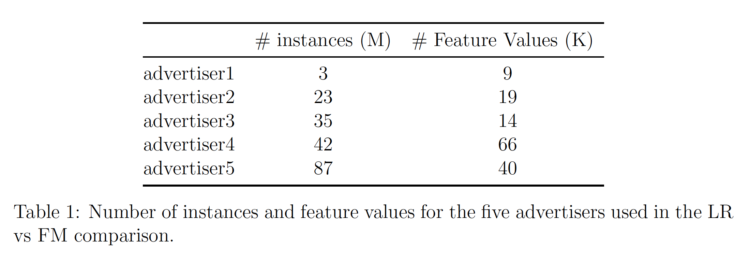
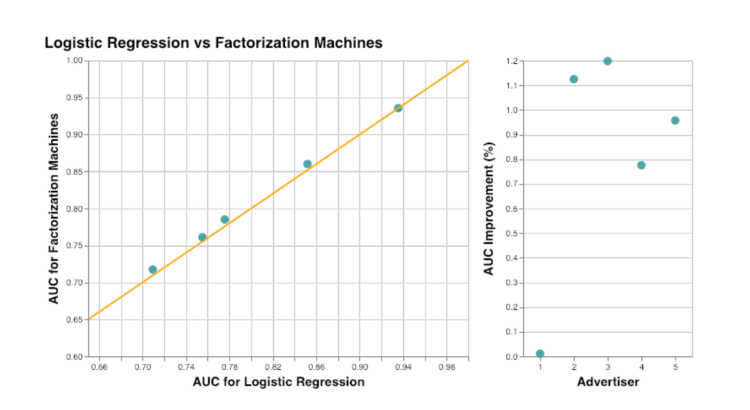
Die AUC-Metrik wurde verwendet, um Factorization Machines mit der logistischen Regression zu vergleichen. Die Ergebnisse sind in Abbildung 3 zusammengefasst. Für einen der Werbetreibenden gab es keine Verbesserung, aber sein AUC war bereits größer als 0,9. Im Durchschnitt (wenn der Ausreißer-Inserent ausgeschlossen wird) verbessert die Verwendung von Factorization Machines den AUC um etwa 1 %. Wie erwartet, sehen wir, dass das Hinzufügen von Informationen über Feature-Interaktionen die Klickvorhersagen verbessert. Und durch die Verwendung von FMs anstelle des manuellen Hinzufügens aller Merkmalskombinationen zur logistischen Regression kann die Komplexität des Modells verringert werden.
Über den Trainingsprozess von FM-Modellen mit AWS Sagemaker berichten wir in einem anderen Beitrag.
Gastautor von:
Inga Silkworth, Leiterin der Datenwissenschaft bei Virtusize, Japan












