En la actualidad, gran parte de la publicidad digital implica la predicción de la probabilidad de un clic o de alguna otra acción del usuario, como una compra. El algoritmo de aprendizaje automático más común para hacer predicciones de la tasa de clics (CTR) es la regresión logística (LR).
Durante la puja en tiempo real (RTB) por un espacio publicitario concreto en una página web, las características, como el navegador, la región, el tipo de dispositivo, etc., son utilizadas por un modelo LR para calcular la probabilidad de clic. Esta probabilidad influye en si se hará una puja y en el importe de la misma. Las predicciones incorrectas pueden dar lugar a un alto coste por clic, lo que se traduce en márgenes bajos y clientes insatisfechos.
La regresión logística es rápida, lo que es importante en la RTB, y los resultados son fáciles de interpretar. Una desventaja de la RL es que es un modelo lineal, por lo que su rendimiento es inferior cuando hay límites de decisión múltiples o no lineales. Por ejemplo, consideremos un caso en el que los datos constan de sólo dos características con dos valores cada una, como se muestra en la figura 1. En este caso es imposible trazar una línea recta de forma que los positivos estén en un lado de la misma y los negativos en el otro. Una forma de evitar esta restricción de linealidad es convertir los vectores de características en un espacio de mayor dimensión introduciendo interacciones de características. Se podría añadir una tercera característica llamada "Dominio de la hora". Esto hace que el espacio de vectores de características sea tridimensional, como se muestra en la figura 2.
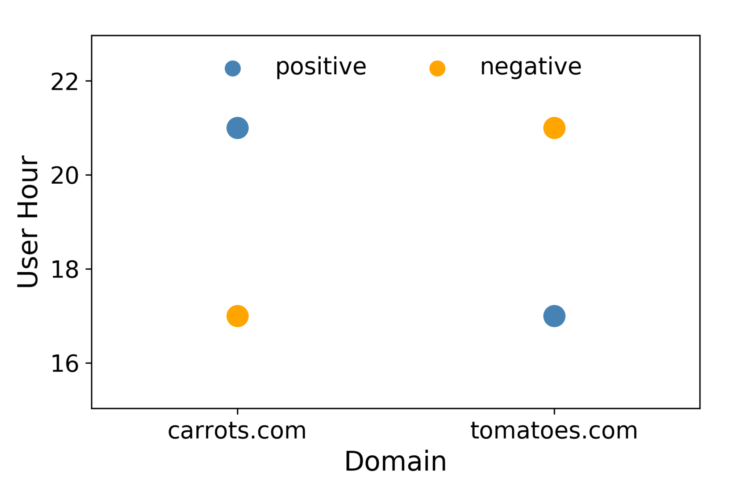
Figura 1: No existe una buena frontera de decisión lineal para este escenario.
Ahora se puede dibujar un plano para separar los positivos de los negativos. Así que con un poco de ingeniería de rasgos podemos hacer que LR aprenda las relaciones entre los pares de rasgos. Sin embargo, esto tiene un precio. Añadir interacciones de características aumenta la complejidad de un modelo a O(n2), donde n es el número total de valores en un conjunto de datos.
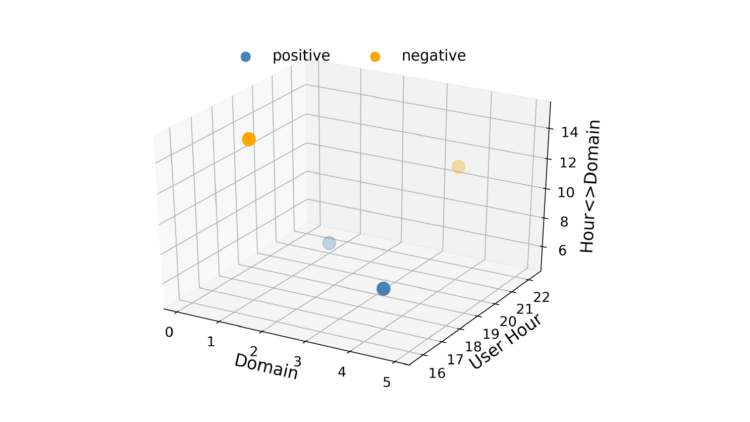
Esto es poco práctico para las predicciones de CTR, donde un modelo podría tener miles de valores. Además, si un par de valores no existe en un conjunto de datos, la regresión logística no podrá aprender su fuerza de interacción. Las máquinas de factorización (FM) [1, 2] abordan estos dos problemas.
¿Qué son las máquinas de factorización?
Para responder a esta pregunta es útil conocer la factorización de matrices, también llamada descomposición de matrices. Se trata simplemente de descomponer una matriz en un producto de varias otras matrices. En otras palabras, la factorización de matrices es simplemente una herramienta matemática para jugar con las matrices y descubrir algo oculto bajo los datos. El análisis de componentes principales (PCA) es un ejemplo de modelo de factorización matricial.
Normalmente no es trivial aplicar un enfoque de factorización a un nuevo problema. Las máquinas de factorización lo hacen mucho más fácil porque pueden conseguir resultados similares a los de otros modelos de factorización simplemente utilizando la ingeniería de características [3]. Echemos un vistazo a la función de coste utilizada en el modelado de predicción lineal del CTR.
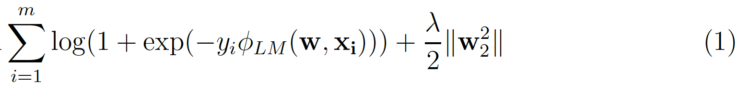
m es el número de (xᵢ, yᵢ) en un conjunto de datos, donde yᵢ es la etiqueta clic/no clic y xᵢ es el nvector de características de dimensión. El segundo término es el término de regularización L₂ donde ƛ es la fuerza de regularización. Para la regresión logística
La adición de interacciones introduce otro término.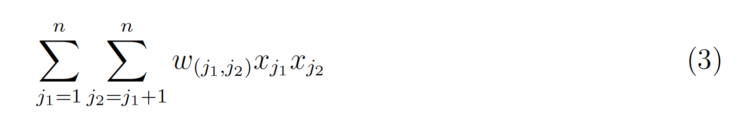
w(j₁ ;j₂) es el peso LR para la interacción, por lo que se aprende un peso para cada par de interacción. El truco de las Máquinas de Factorización es aprender un kvector latente para cada característica, donde k es un parámetro especificado por el usuario. El efecto de la interacción puede calcularse simplemente tomando el producto interno de los dos vectores.
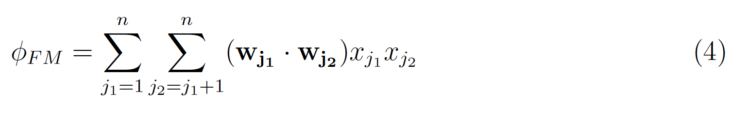
que puede reescribirse como
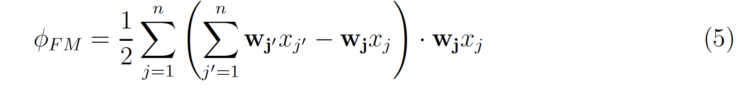
La complejidad de la ecuación anterior es sólo O(nk), donde n es el número medio de valores distintos de cero por instancia.
Regresión logística frente a máquinas de factorización
Hemos utilizado la implementación de AWS Sagemaker de Máquinas de Factorización para probar FM en nuestros datos. La información sobre los datos de los cinco anunciantes diferentes analizados figura en la Tabla 1.
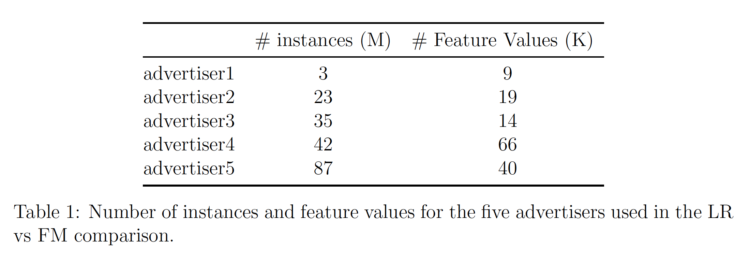
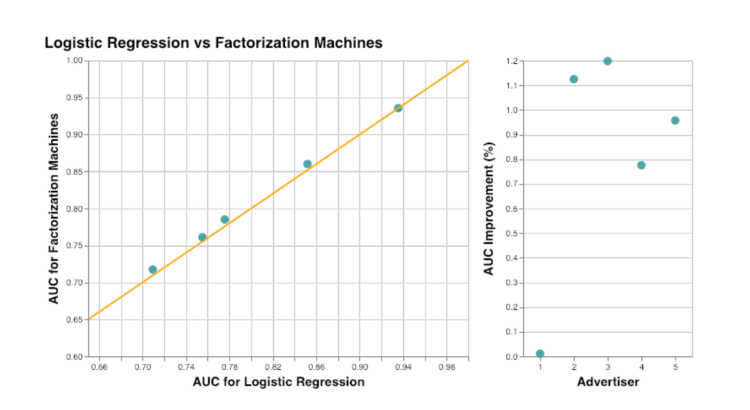
Se utilizó la métrica AUC para comparar las Máquinas de Factorización con la Regresión Logística. Los resultados se resumen en la Figura 3. Uno de los anunciantes no experimentó ninguna mejora, pero su AUC ya era superior a 0,9. Por término medio (si se excluye el anunciante atípico), el uso de Máquinas de Factorización mejora el AUC en aproximadamente un 1%. Como se esperaba, vemos que añadir información sobre las interacciones de las características mejora las predicciones de clics. Además, al utilizar las máquinas de factorización en lugar de añadir manualmente todas las combinaciones de características a la regresión logística, se puede reducir la complejidad del modelo.
Informamos sobre el proceso de entrenamiento de los modelos FM utilizando AWS Sagemaker en otro post.
Con autoría de:
Inga Silkworth, Directora de Ciencia de Datos de Virtusize, Japón












