En el aprendizaje automático (ML), el rendimiento del modelo se ve afectado tanto por los datos como por el algoritmo de aprendizaje que se elija. En general, cabe esperar que cuantos más datos (buenos) se recojan, más información se podrá extraer y mejor será el rendimiento del modelo. Sin embargo, existe un punto de saturación en el que el rendimiento del modelo deja de mejorar incluso con datos adicionales. Esta saturación se produce cuando el tamaño de los datos no puede ayudar a un modelo a superar los supuestos del algoritmo de aprendizaje. Por ejemplo, cuando se utiliza un modelo lineal para clasificar datos en los que reside una relación no lineal, nunca se alcanzará la predicción perfecta, incluso con muchos datos de entrenamiento.
Veamos un ejemplo de cómo el tamaño de los datos de entrenamiento afecta al rendimiento del modelo de ML.
En la publicidad online, es fundamental estimar la probabilidad de que un usuario responda a un anuncio (ya sea un clic o una conversión). Esta probabilidad indica el interés del usuario por un producto o una marca, y obtener una predicción precisa mejora tanto la experiencia del usuario como la eficacia de la campaña publicitaria. Para predecir el porcentaje de clics (CTR), se suelen utilizar algoritmos lineales como la regresión logística (LR), y aquí veremos cómo el tamaño de los datos afecta al rendimiento de la LR. También veremos los resultados de las máquinas de factorización (FM), un algoritmo eficaz para añadir características cruzadas a la LR. Aquí nos concentraremos en el efecto del tamaño de los datos sobre el rendimiento del modelo, y dejaremos la comparación del rendimiento entre LR y FM para otro artículo.
Nuestros datos proceden de 5 anunciantes; la tabla siguiente muestra el número de entradas y el número de características de cada uno:
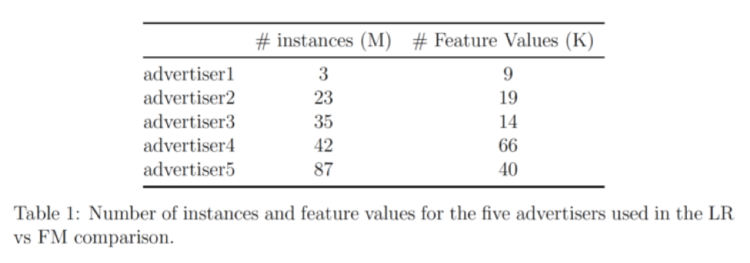
Este conjunto de datos se preprocesa y se muestrea aleatoriamente en grupos de datos de diferentes tamaños. A continuación, se aplican por separado LR y FM a cada grupo de datos para generar modelos de clasificación, y se evalúan los modelos en conjuntos de datos de prueba que se han dejado fuera utilizando Puntuaciones AUC.
Las figuras siguientes muestran la relación entre el rendimiento del modelo y el tamaño de los datos. El eje horizontal representa la fracción de muestreo, por ejemplo, 0,1 significa que se utiliza el 10% de los datos para el entrenamiento. El eje vertical indica el rendimiento del modelo (es decir, el AUC). Los valores de AUC se sitúan en rangos diferentes para los distintos anunciantes, lo que dificulta la comparación. Para tener una comparación más clara, reescalamos el AUC para cada anunciante con la siguiente regla:
AUC_rescalado = (AUC / AUC_avg - 1) * 100%
donde AUC_avg es el AUC promediado en todas las fracciones de muestreo para ese anunciante.
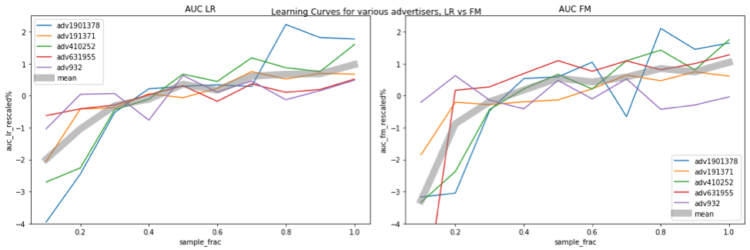
En el gráfico, los diferentes anunciantes están codificados por colores, y la curva gris gruesa representa la media del AUC reescalado de los 5 anunciantes. Las figuras de la izquierda y la derecha muestran los resultados de LR y FM, respectivamente. Está claro que el rendimiento del modelo sigue aumentando cuando se utilizan más datos para el entrenamiento, y con la cantidad de datos utilizados en la prueba, ni LR ni FM alcanzan los niveles de saturación. Una cosa que merece la pena mencionar es que, cuando aumentamos el tamaño de los datos de entrenamiento, el espacio de características también se amplía, por lo que la complejidad del modelo aumenta, lo que hace más difícil la saturación.
También hay una tendencia interesante: el AUC aumenta aproximadamente un 1% cuando el tamaño de los datos casi se duplica. Esta relación es probablemente más clara si hacemos un gráfico lin-log trazando el eje x en escala logarítmica, y ahora vemos una línea gris recta (más o menos, al menos para LR), lo que significa que cuando aumentamos x (tamaño de los datos) exponencialmente, y (rendimiento) aumenta en una cantidad lineal.
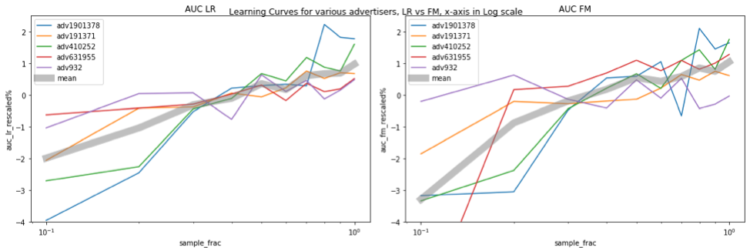
En resumen, en nuestro experimento, el punto de saturación nunca se alcanzó con cantidades crecientes de datos. Cuando el tamaño de los datos se duplica, el AUC aumenta casi un 1%. Para las aplicaciones industriales, un aumento del 1% en el AUC suele considerarse una mejora significativa. Esto sirve para argumentar que, cuando hay suficientes datos, aumentar el tamaño del entrenamiento es una forma directa de mejorar el rendimiento del modelo.




